FlowPlot

Create beautiful plots of the CRLD flow in phase space

Examples

from pyCRLD.Agents.StrategyActorCritic import stratAC
from pyCRLD.Environments.SocialDilemma import SocialDilemma

from pyCRLD.Utils import FlowPlot as fp

import numpy as np
np.random.seed(0)

env = SocialDilemma(R=1.0, T=0.8, S=-0.5, P=0.0)
mae = stratAC(env=env, learning_rates=0.1, discount_factors=0.9)
x = ([0], [0], [0])
y = ([1], [0], [0])
flowarrow_points = np.linspace(0.01 ,0.99, 9)
standards = [mae, x, y, flowarrow_points]

Standard quiver flowplot

showing reward-predition error arrows

ax = fp.plot_strategy_flow(*standards)
ax[0].set_xlabel("Agent 0's cooperation probability")
ax[0].set_ylabel("Agent 1's cooperation probability");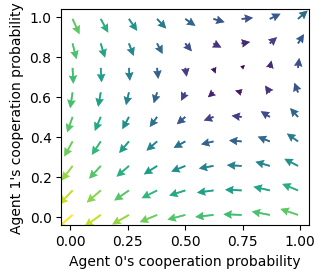

Standard quiver flowplot with trajectory

ax = fp.plot_strategy_flow(*standards)
ax[0].set_xlabel("Agent 0's cooperation probability")
ax[0].set_ylabel("Agent 1's cooperation probability")

X = mae.random_softmax_strategy()
trj, fpr = mae.trajectory(X, Tmax=1000, tolerance=1e-6)
print("Trajectory length:", len(trj))
fp.plot_trajectories([trj], x, y, fprs=[fpr], axes=ax);

Trajectory length: 287

Quiver plot with strategy differences

Notices how the edges of the phase space differ compared to the plots with reward-prediction errors above.

ax = fp.plot_strategy_flow(*standards, use_RPEarrows=False)
ax[0].set_xlabel("Agent 0's cooperation probability")
ax[0].set_ylabel("Agent 1's cooperation probability");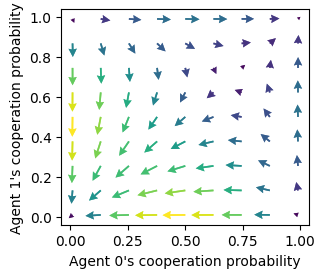

Streamplot w RPE

with reward-prediciton errors

ax = fp.plot_strategy_flow(*standards, kind="streamplot")
ax[0].set_xlabel("Agent 0's cooperation probability")
ax[0].set_ylabel("Agent 1's cooperation probability");
ax[0].set_xlim(0, 1); ax[0].set_ylim(0, 1);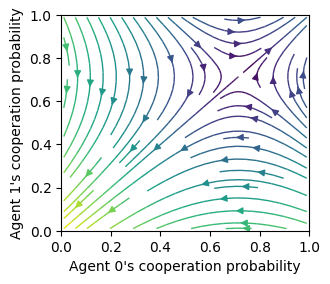

Streamplot w dX

with strategy differences

ax = fp.plot_strategy_flow(*standards, kind="streamplot", use_RPEarrows=False)
ax[0].set_xlabel("Agent 0's cooperation probability")
ax[0].set_ylabel("Agent 1's cooperation probability");
ax[0].set_xlim(0, 1); ax[0].set_ylim(0, 1);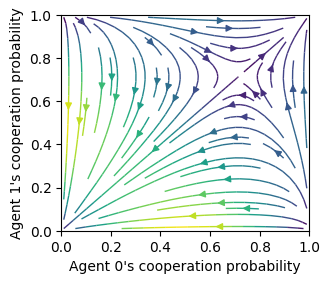

Core methods

---

source

plot_strategy_flow

 plot_strategy_flow (mae, x:tuple, y:tuple, flowarrow_points,
                     NrRandom:int=3, use_RPEarrows=True, col:str='LEN',
                     cmap='viridis', kind='quiver+samples', sf=0.5,
                     lw=1.0, dens=0.75, acts=None, conds=None,
                     axes:Iterable=None, verbose=False)

Create a flow plot in strategy space.

	Type	Default	Details
mae			CRLD multi-agent environment object
x	tuple		which phase space axes to plot along x axes
y	tuple		which phase space axes to plot along y axes
flowarrow_points			specify range & resolution of flow arrows
NrRandom	int	3	how many random (in the other dimensions) stratgies for averaging
use_RPEarrows	bool	True	Use reward-prediction error arrows?, otherwise use strategy differences
col	str	LEN	color indicates either strength of flow via colormap, otherwise a fixed color name
cmap	str	viridis	Colormap
kind	str	quiver+samples	Kind of plot: “streamplot”, “quiver+samples”, “quiver”, …
sf	float	0.5	Scale factor for quiver arrows
lw	float	1.0	Line width for streamplot
dens	float	0.75	Density for streamplot
acts	NoneType	None	Action descriptions
conds	NoneType	None	Conditions descriptions
axes	Iterable	None	Axes to plot into
verbose	bool	False	shall I talk to you while working?

---

source

plot_trajectories

 plot_trajectories (Xtrajs:Iterable, x:tuple, y:tuple,
                    cols:Iterable=['r'], alphas:Iterable=[1.0],
                    lss:Iterable=['-'], lws:Iterable=[2],
                    mss:Iterable=[None], msss:Iterable=[0],
                    fprs:Union[Iterable,bool]=None,
                    plot_startmarker:bool=True, axes:Iterable=None,
                    submean:bool=False)

Plot multiple trajectories in phase space.

	Type	Default	Details
Xtrajs	Iterable		Iterable of phase space trajectories
x	tuple		which phase space axes to plot along x axes
y	tuple		which phase space axes to plot along y axes
cols	Iterable	[‘r’]	Colors to iterate through
alphas	Iterable	[1.0]	Alpha values to iterate through
lss	Iterable	[‘-’]	Linestyles to iterate through
lws	Iterable	[2]	Linewidths to iterate through
mss	Iterable	[None]	Endmarkers to iterate through
msss	Iterable	[0]	Endmarker sizes to iterate through
fprs	Union	None	Iteralbe indicating which trajectories reached a fixed point
plot_startmarker	bool	True	plot a marker at the initial condition
axes	Iterable	None	Axes to plot into
submean	bool	False

Helpers

---

source

_checks_and_balances

 _checks_and_balances (x:tuple, y:tuple)

Check the format of the x and y parameter.

	Type	Details
x	tuple	which phase space axes to plot along x axes
y	tuple	which phase space axes to plot along y axes
Returns	tuple	(lengths for each dimension, index of dimension to iter, length of iter)

Let’s say we want to plot the probability of cooperation of the 0th agent on the \(x\) axis and of the 1st agent on the \(y\) axis for states 2,3 and 5, we specify (assuming the cooperation is the 0th action)

x = ([0], [2,3,5], [0])
y = ([1], [2,3,5], [0])
_checks_and_balances(x, y)

(array([1, 3, 1]), 1, 3)

---

source

_prepare_axes

 _prepare_axes (axes:Iterable, xlens:tuple)

Check whether axes have been provided correctly. If axes haven’t been provided, provide them.

	Type	Details
axes	Iterable	Axes to plot into
xlens	tuple	Lengths for each dimension of x and y
Returns	Iterable	of matplotlib axes

_prepare_axes(None, [1,3,1])

array([<Axes: >, <Axes: >, <Axes: >], dtype=object)

---

source

_dXisa_s

 _dXisa_s (Xisa_s:Iterable, mae)

Compute Xisa(t-1)-Xisa(t) for all Xisa_s.

	Type	Details
Xisa_s	Iterable	of joint strategies Xisa
mae		CRLD multi-agent environment object
Returns	ndarray	joint strategy differences

from pyCRLD.Agents.StrategyActorCritic import stratAC
from pyCRLD.Environments.SocialDilemma import SocialDilemma

env = SocialDilemma(R=1.0, T=0.8, S=-0.5, P=0.0)
mae = stratAC(env=env, learning_rates=0.1, discount_factors=0.9)

Xisa_s = [mae.random_softmax_strategy() for _ in range(7)]
_dXisa_s(Xisa_s, mae).shape

(7, 2, 1, 2)

---

source

_dTDerror_s

 _dTDerror_s (Xisa_s:Iterable, mae)

Compute reward-prediction errors TDerror_s for Xs.

	Type	Details
Xisa_s	Iterable	of joint strategies Xisa
mae		CRLD multi-agent environment object
Returns	ndarray	joint reward-prediction errors

env = SocialDilemma(R=1.0, T=0.8, S=-0.5, P=0.0)
mae = stratAC(env=env, learning_rates=0.1, discount_factors=0.9)

Xisa_s = [mae.random_softmax_strategy() for _ in range(7)]
_dTDerror_s(Xisa_s, mae).shape

(7, 2, 1, 2)

---

source

_strategies

 _strategies (mae, xinds:tuple, yinds:tuple, xval:float, yval:float,
              NrRandom)

Creates strategies (as a particular type of phase space item) for one ax plot point. All strategies have value xval at the xinds index and value yval at the yinds.

	Type	Details
mae		CRLD multi-agent environment object
xinds	tuple	of indices of the phase space item to plot along the x axis
yinds	tuple	of indices of the phase space item to plot along the y axis
xval	float	the value of the phase space item to plot along the x axis
yval	float	the value of the phase space item to plot along the y axis
NrRandom		how many random (in the other dimensions) stratgies for averaging
Returns	ndarray	Array of joint strategies

For example, given

env = SocialDilemma(R=1.0, T=0.8, S=-0.5, P=0.0)
mae = stratAC(env=env, learning_rates=0.1, discount_factors=0.9)

the following parameters give

xinds = (0, 0, 0)  # Plot agent 0's state-action item 0, 0
yinds = (1, 0, 0)  # Plot agent 1's state-action item 0, 0
NrRandom = 3

strats = _strategies(mae, xinds, yinds, xval=0.2, yval=0.4, NrRandom=NrRandom)
assert strats.shape[0] == NrRandom
strats.shape

(3, 2, 1, 2)

The first dimension of the _strategies return holds the randomization in the other dimensions than given by xinds and yinds. Note that the randomization in the other dimensions makes no sense in a stateless normal-form game since there are no other dimensions.

---

source

_data_to_plot

 _data_to_plot (mae, flowarrow_points:Iterable, xinds:tuple, yinds:tuple,
                NrRandom:int, difffunc:collections.abc.Callable,
                phasespace_items:collections.abc.Callable, verbose=False)

	Type	Default	Details
mae			CRLD multi-agent environment object
flowarrow_points	Iterable		range & resolution of flow arrows
xinds	tuple		of indices of the phase space object to plot along the x axis
yinds	tuple		of indices of the phase space object to plot along the y axis
NrRandom	int		how many random (in the other dimensions) stratgies for averaging
difffunc	Callable		to compute which kind of arrows to plot (RPE or dX)
phasespace_items	Callable		to obtain phase space items for one ax plot point
verbose	bool	False	shall I talk to you while working?
Returns	tuple		meshgrid for (X, Y, dX, dY)

For example, given

env = SocialDilemma(R=1.0, T=0.8, S=-0.5, P=0.0)
mae = stratAC(env=env, learning_rates=0.1, discount_factors=0.9)

the following parameters give

xinds = (0, 0, 0)  # Plot agent 0's state-action item 0, 0
yinds = (1, 0, 0)  # Plot agent 1's state-action item 0, 0
flowarrow_points = np.array([0.1, 0.3, 0.5, 0.7, 0.9])
NrRandom=7
difffunc = _dTDerror_s
phasespace_items = _strategies
verbose = True

X, Y, dX, dY = _data_to_plot(mae, flowarrow_points, xinds, yinds, NrRandom, difffunc,
                             phasespace_items=_strategies, verbose=verbose)

assert X.shape == Y.shape; print("\nShape of `X` and `Y`:", X.shape)
assert dX.shape == dY.shape; print("Shape of `dX` and `dY`:", dX.shape)
assert dX.shape[-1] == NrRandom

 [plot] generating data 96 %   
Shape of `X` and `Y`: (5, 5)
Shape of `dX` and `dY`: (5, 5, 7)

Let \(l\) be the number of the flowarrow_points, than X and Y have shape of (\(l\), \(l\)). dX and dY have shape of (\(l\), \(l\), Number of randomizations).

---

source

_plot

 _plot (dX:numpy.ndarray, dY:numpy.ndarray, X:numpy.ndarray,
        Y:numpy.ndarray, ax=None, sf=1.0, col='LEN', cmap='viridis',
        kind='quiver+samples', lw=1.0, dens=0.75)

Plots the flow for one condition into one axes

	Type	Default	Details
dX	ndarray		differences in x dimension
dY	ndarray		differences in y dimension
X	ndarray		meshgrid in x dimension
Y	ndarray		meshgrid in y dimension
ax	NoneType	None	Individual axis to plot into
sf	float	1.0	Scale factor for quiver arrows
col	str	LEN	what should the color indicatie
cmap	str	viridis	Colormap
kind	str	quiver+samples	Kind of plot: “quiver”, “quiver+samples”, “quiver”, …
lw	float	1.0	Line width
dens	float	0.75	Density

---

source

_scale

 _scale (x:float, y:float, a:float)

Scales length of the (x, y) vector accoring to length to the power of a.

	Type	Details
x	float	x dimension
y	float	y dimension
a	float	scaling factor
Returns	tuple	scaled (x,y)

A scale factor of 0 makes all vectors equally large.

_scale(4, 3, 0)

(0.8, 0.6000000000000001)

_scale(40, 30, 0)

(0.8, 0.6)

A scale factor of 1 does not change a vector’s length

_scale(4, 3, 1)

(4.0, 3.0)

_scale(40, 30, 1)

(40.0, 30.0)